Részletes kutatási terv
A 2017-től 2022-ig terjedő időszakban kutatócsoportunk a járműdinamika alapkutatási problémáira fókuszál; ezen a területen nemzetközi szintű eredményeket értünk el a korábbi években. Két olyan téma kerül előtérbe, melyek iránt mind az ipar, mind a tudományos közösség részéről kitüntetett érdeklődést tapasztaltunk: a dinamikai érintkezési feladatok és az alulaktuált mechanikai rendszerek vizsgálata. A munka hatékony szervezése érdekében két munkacsomagot jelöltünk ki.
Tartalom 1. munkacsomag (MCs1): Dinamikai érintkezési feladatok 2. munkacsomag (MCs2): Alulaktuált mechanikai rendszerek A várható eredmények jelentősége, alkalmazási lehetőségei Irodalomjegyzék
1. munkacsomag (MCs1): Dinamikai érintkezési feladatok
Motiváció
Egyre nagyobb az igény a mechanikai érintkezés és súrlódás megbízható modellezésére, mert e nélkül nem lehetséges a szerkezetek elegendően pontos modális analízise és stabilitásvizsgálata. Ebben a témakörben a kutatócsoport tervezett vizsgálatai több egymást kiegészítő, az absztrakt matematikai elmélettől a gyakorlati alkalmazásokig terjedő modellezési szintet ölelnek fel.
A súrlódás hatását leggyakrabban a klasszikus Coulomb-modell alapján veszik figyelembe, a mérnöki gyakorlatban viszont általában a viszkózus csillapítási modellt használják a modális analízis során. A kutatási irányok egyike a klasszikus Filippov-féle nemsima analízis alkalmazása a súrlódásos kapcsolatok vizsglatára [1]. Ugyanakkor a kutatócsoport által továbbfejlesztett szakirodalmi eredmények [2] szerint a testek rugalmassága következtében a súrlódási munka jelentősen függ a testeket összeszorító erő eloszlásától. Következésképpen, a testek térbeli érintkezésének megfelelő jellemzése lehetőséget nyújthat olyan ekvivalens csillapítási tényezők meghatározására, melyek Coulomb-súrlódás jelenlétében is használhatók a modális analízis során.
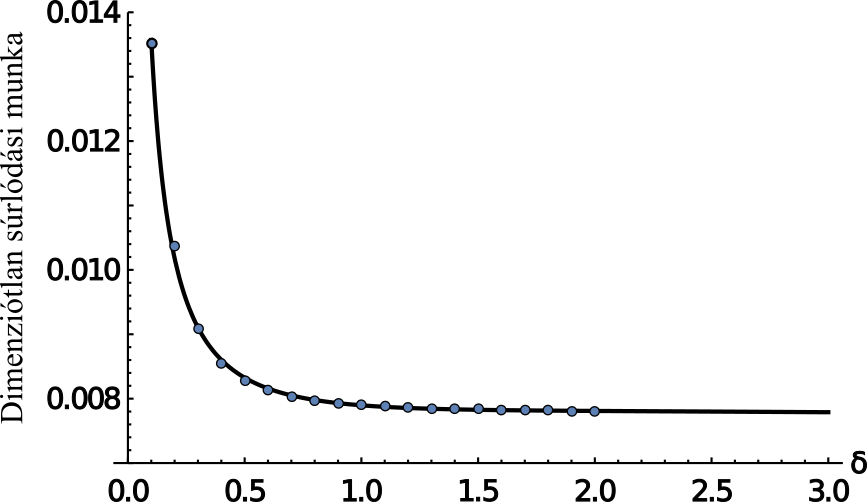
1. ábra. Súrlódási munka a Gauss-görbe alakú terhelés eloszlás szórásának függvényében
Két test érintkezése során csupán a felületi egyenetlenségek csúcsai kerülnek kölcsönhatásba, ezért erő csak a látszólagos érintkező terület töredékén tud átadódni. Ezen a kis területen kémiai reakciók indulnak meg, melyek az érintkezés minőségét időtől függővé teszik. A csúszási és tapadási súrlódási együtthatók eltérő nagysága is erre vezethető vissza [3]. Mikroszkopikus méretekben tehát nagyon bonyolult az érintkezéshez és súrlódáshoz köthető folyamatok figyelembevétele. Számos elmélet és számítási módszer található a szakirodalomban pontosan feltérképezett felületi topológiájú testek érintkezésének modellezésére. Ezek a módszerek általában csak kis felületek vizsgálatára alkalmasak, makroszkopikus méretekben nem alkalmazhatók a túlzott adattárolási és számítási igényük miatt és a kapott eredményeket nehéz kísérletileg ellenőrizni. Az ipar részéről egyre nagyobb az igény olyan módszerek kidolgozására, melyekkel megbízhatóan jellemezhető gépek és járművek alkatrészeinek érintkezése. Ezért a munkacsomag egyik legfontosabb feladata az érintkezés merevségre és csillapításra gyakorolt hatásainak elemzése. Feltevésünk szerint ehhez elegendő a felületi minőség és erő eloszlás megfelelő pontosságú ismerete. A felületi minőség mérésére rendelkezésre áll a méréstechnikai háttér, a felületi erő eloszlás pedig egy új, a BME Műszaki Mechanikai Tanszéken kidolgozott eljárás segítségével határozható meg.

2. ábra. Az érintkezés vizsgálatára kifejlesztett mérőberendezés
Mind a Coulomb-súrlódás nemsima modelljeinek vizsgálata, mind az érintkezés modális tulajdonságokra gyakorolt hatásainak meghatározása természetesen kapcsolódik a járműdinamika gördülési problémáihoz. A kutatócsoport a kerék-talaj kapcsolat területén végzett kutatásai során már foglalkozott a dinamikus érintkezési feladatokkal. Gördülés során a kerék-talaj érintkezési tartományban tapadó és csúszó zónák jönnek létre, melyek még a kerék konstans sebességgel történő gördülése során sem feltétlenül állandósulnak. Bár kifinomult számítógépes szimulációk segítségével figyelembe vehető az érintkezés időben változó jellege, a jelentős számítási igény a gyakorlatban nem teszi lehetővé az ilyen szimulációk eredményes felhasználását. Lehetséges azonban az érintkezési zónák kevésbé aprólékos leírása is, ha a tapadó illetve csúszó zónákra valamilyen közelítő megoldás állítható elő. Ez esetben csupán a zónák létezésének vizsgálatára és határainak meghatározására kell megfelelő eljárást kidolgozni. Vontatott kerék esetére a kutatócsoport tagjai már készítettek ilyen numerikus algoritmust, melyet hatékonyan alkalmaztak a kerék szitáló mozgásának elemzésekor [4].
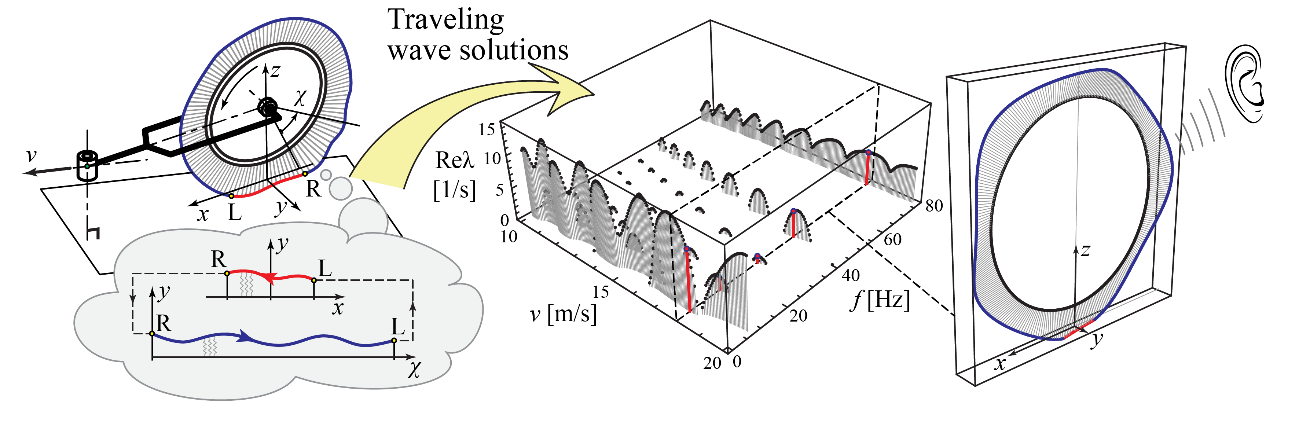
3. ábra. A vontatott kerék modellje és a rezgési frekvenciák sebességfüggése
Az ismertetett problémákhoz kötődő tervezett kutatási feladatokat az alábbiakban részletezzük.
MCs1.1: Az érintkezés merevségre és csillapításra gyakorolt hatásainak modellezése
A következő pályázati időszakban fontos kutatási cél olyan algoritmusok felállítása, melyekkel az erő eloszlás ismeretéből kiindulva következtetni lehet az érintkezés merevségére és csillapítására. A vizsgálatok kezdeti szakaszában egyszerű, néhány szabadsági fokú mechanikai modellek felállítására kerül sor. Az érintkezési merevség értékét analitikus módszerekkel tervezzük számítani, a disszipált energia kiszámításához viszont már numerikus módszerekre lesz szükség. További cél az érintkezés tulajdonságainak koncentrált paraméterű leírása – azaz olyan elemek definiálása a mechanikai modellekben, melyek néhány paraméter segítségével jól leírják az érintkezés és a súrlódás modális paraméterekre gyakorolt hatását. Ehhez végeselem módszeres számítások futtatását is tervezzük, melyhez megfelelő alapot nyújtanak Barber és szerzőtársai eredményei [5].
MCs1.2: Rezgésdiagnosztikai rendszer építése és az érintkezés kísérleti modális analízise
A kutatás során nagy hangsúlyt fektetünk az elméleti eredmények kísérleti igazolására is. Ehhez elsősorban a modális analízis eszköztárát kívánjuk használni, mellyel megvizsgálható egy szerkezet rezgéstani válasza különböző gerjesztésekre. A gerjesztők alkalmazása és illesztése azonban nem triviális feladat, ha a gerjesztést gyorsan mozgó, pl. forgó alkatrészekre kell alkalmazni, mint amilyenek a gördülőcsapágyak vagy a járművek kerekei. Ennek a speciális feladatnak a megoldásához tervezzük egy több elemből felépülő, rugalmasan alkalmazható rezgésdiagnosztikai rendszer kialakítását; mindehhez a befogadó tanszék rezgéslaboratóriuma megfelelő infrastruktúrát biztosít.
A probléma komplexitása miatt szükség lehet olyan további kísérleti módszerek kidolgozására is, melyekkel adott alkatrészek esetében gyorsan becsülhetők az érintkezés modális tulajdonságok szempontjából releváns jellemzői. Érintkezési problémák esetén az érintkező felületek közti súrlódás vagy a fellépő kontaktmerevség hatására az ilyen rendszerek bonyolult, nemlineáris viselkedést mutatnak. Mivel ekkor a rezgéstani jellemzők függenek a rezgés amplitúdójától is, nem elegendő a jellemző frekvenciákat vizsgálni, szükség van a gerjesztések kontrollált alkalmazására amplitúdó és frekvencia szempontjából is, ezért tervezzük az ehhez szükséges speciális gerjesztő berendezések kialakítását.
MCs1.3: A kerék-talaj kapcsolat „emlékező” jellegének kísérleti kimutatása
A kerék-talaj érintkezési modell finomítása után tervezzük a vontatott kerék vizsgálata kapcsán elért elméleti eredmények kísérleti igazolását. A rendelkezésre álló kísérleti berendezés átépítése után lehetőség nyílik a nagy amplitúdójú periodikus mozgások gyakorlatban történő detektálására. Az eredmények igazolhatnák azt a sejtést, hogy a vontatott kerekekre jellemző bistabil viselkedés (egyszerre létezik stabil egyenes vonalú gördülés és nagy amplitúdójú szitálás) nem a csapágyban megjelenő száraz súrlódásnak, hanem a kerék-talaj kapcsolat „emlékező” jellegének tulajdonítható. Ez azt jelenti, hogy a kerék egy pontjának letapadása információt hordoz a kerék korábbi állapotával kapcsolatban, azonban megcsúszáskor ez az információ elvész. A kutatócsoport tagjai kísérletet tesznek az instabil periodikus mozgások gyakorlatban való érzékelésére. Ennek a világviszonylatban is mérföldkőnek számító feladatnak a megoldását a kutatócsoport kerékdinamikában és szabályozástechnikában jártas tagjainak kooperációja teszi lehetségessé.
MCs1.4: Többzónás érintkezési modell alkalmazása
A kutatás további részében a mind elméletileg, mind kísérletileg kidolgozott többzónás, „emlékező/felejtő” érintkezési modell kerül alkalmazásra különböző járműdinamikai és gépészeti feladatokban. Ezáltal lehetővé válik a kerék-talaj kapcsolat esetén a hosszirányú deformációk pontosabb leírása, amely a hirtelen terhelésváltások (fékezés-gyorsítás) során lejátszódó dinamikai jelenségeket magyarázhatja. Emellett az összetettebb járműmodellek nemlineáris vizsgálatára vagy a gördülőcsapágyakban lezajló folyamatok megismerésére is lehetőség nyílik a hatékonyabb érintkezési modell használatával.
2. munkacsomag (MCs2): Alulaktuált mechanikai rendszerek
Motiváció
Alulaktuáltságról akkor beszélhetünk, ha az aktuátorok (beavatkozók) száma kisebb a mechanikai rendszer szabadságfokainak a számánál. Ilyenek például a daruk, melyeknél a függesztő kábel felső végpontjának pozíciója közvetlenül szabályozható, a lengő teher azonban a dinamikai viselkedése által megszabott mozgást végzi.
Kutatócsoportunkban számos vizsgálati módszert fejlesztettünk ki alulaktuált robotok tervezésére és elemzésére [6,7]. A szabályozás során átkapcsolások történnek a megkívánt mozgást biztosító és a belső dinamika stabilitását biztosító szabályozások között, azaz a rendszer dinamikája nemsima jellegű lesz. A következő időszakban a kidolgozott módszereket tervezzük alkalmazni más területeken is.
Számos mechanikai rendszernek hasonló tulajdonságai vannak, mint az alulaktuált robotoknak – például ilyenek a járműszerelvények. A jármű és vontatmány esetében ez különösen fékezés vagy tolatás esetében szembetűnő. Az ember mozgását elősegítő külső robotikai vázak, az ún. exoskeletonok és a két lábon közlekedő robotok is ebbe a kategóriába sorolhatók. Az emberi járás és futás folyamatának vizsgálatával nyerhető eredmények hozzájárulhatnak az exoskeletonok és robotok fejlesztéséhez, azok gyakorlati alkalmazása elsősorban az energiahatékonyság javítását segíti elő.
Az alulaktuált rendszerek számítógépes szabályozása során jelentős lehet a digitális hatások szerepe a dinamikai viselkedésben. Már kis kerekítési hibák is ahhoz vezethetnek, hogy a stabil tartomány határa közelében nagyon megnő a szabályozási hiba a különös attraktorokat és repellorokat tartalmazó fázistérbeli struktúra miatt [8]. Mivel a „külső” és „belső” szabályozó dinamika közötti átkapcsolásoknak hasonló hatása lehet mint a kerekítésnek, ennek vizsgálatát is tervezzük a következő pályázati ciklusban.
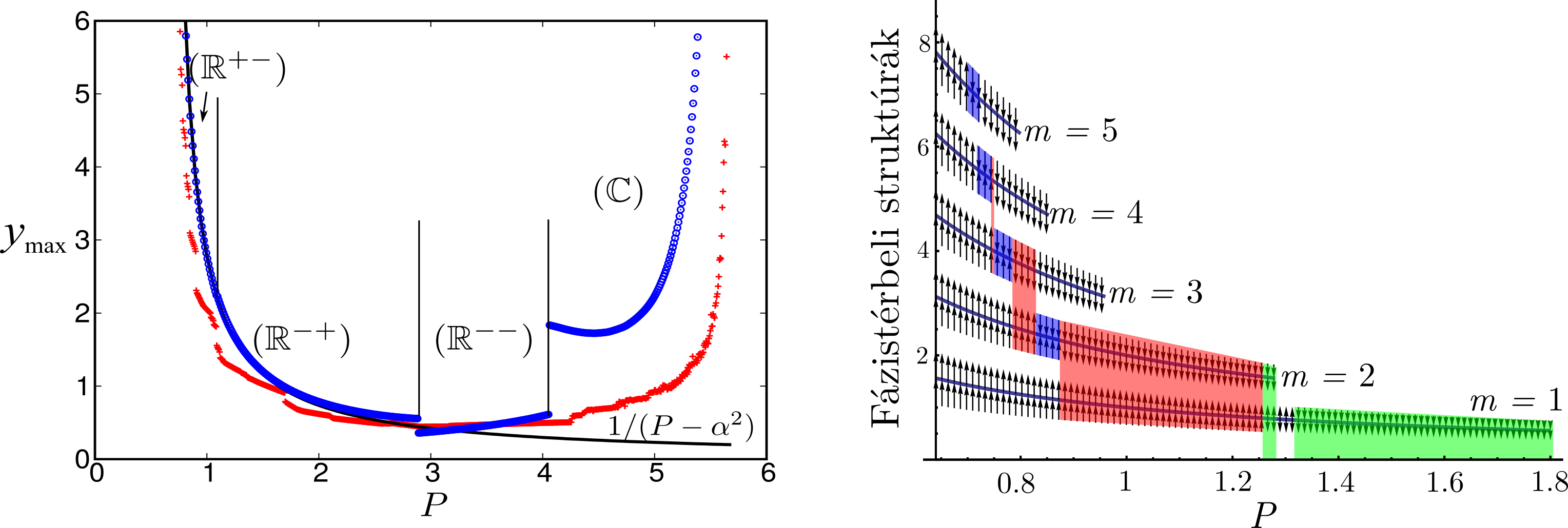
4. ábra. A szabályozási hibának és a fázistérbeli struktúrák elhelyezkedésének függése az erősítési tényezőtől
MCs2.1: Alulaktuált járműszerelvények modellezése
A személygépjárművek esetében egyre jobban elterjednek a tolatást segítő vagy a parkolást automatikusan végrehajtó alkalmazások. Ugyanennek a feladatnak a megoldása azonban egy pótkocsis teherautó esetén bonyolult alulaktuált-anholonom feladathoz vezet. Számos kutatóintézet és gépjárműgyár is foglalkozik ezzel a problémával, amit általában plusz beavatkozó szervvel próbálnak feloldani [9]. Célunk olyan megoldás kifejlesztése, amihez nem szükséges az eredeti berendezés módosítása.
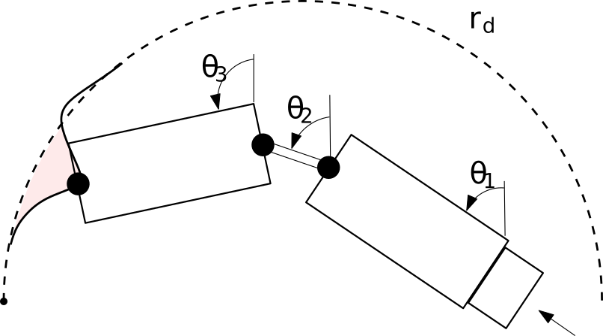
5. ábra. Pótkocsis járműszerelvény tolatása
Vontatott járműveknél nehézséget okoz a biztonságos fékezés kivitelezése és az ABS rendszerek megfelelő modellezése. Dinamikai vizsgálati módszereink természetes módon kiterjeszthetők ezekre a nagy szabadságfokú anholonom rendszerekre is. Célunk, hogy a korábbiakban kifejlesztett, differenciál-algebrai rendszerek stabilitását vizsgáló technikát kiterjesszük olyan rendszerekre, melyek nagy szabadsági fokúak – ilyenek például az ABS-szel fékezett vontatmányok. A járműdinamikai alkalmazások mellett módszereink további területeken is alkalmazhatóak, a matematikai modellek hasonlóságai miatt.
MCs2.2: Alulaktuált mobil robotok vizsgálata
Noha az emberi testet több száz izom mozgatja, azt több okból is tekinthetjük alulaktuáltnak. Egyrészt nem áll rendelkezésre semmiféle külső erő az orientáció és a súlypont röppályájának módosítására a futáskor fellépő repülő fázisban, másrészt az emberi mozgás során az egyes testrészek lendülő mozgást végeznek az izmok működtetése nélkül. Az emberi járást utánzó passzív lépegetők is az ilyen jellegű mozgást használják ki az energiahatékony helyváltoztatáshoz. Ezért tervezzük megvizsgálni az alulaktuáltság alkalmazásának lehetőségét exoskeletonok és lábon közlekedő robotok esetében az energiahatékonyság javítása érdekében.
MCs2.3: Talaj-láb ütközés modellezése
Az alulaktuáltság mellett a járás és futás vizsgálatánál felmerülő másik kihívás a talaj-láb ütközés modellezése. Korábbi számítási eredményeinket [10] arra alapoztuk, hogy a talajjal történő érintkezéskor a sebességállapot ugrásszerűen változik meg. Céljaink között szerepel pontosabb ütközési modell beépítése a többtest-dinamikai modellbe, amelyet a futást végző személyre, exoskeletonra vagy robotra alkalmazunk. Az ütközési modell felhasználható mesterséges lábfej kialakításánál is.
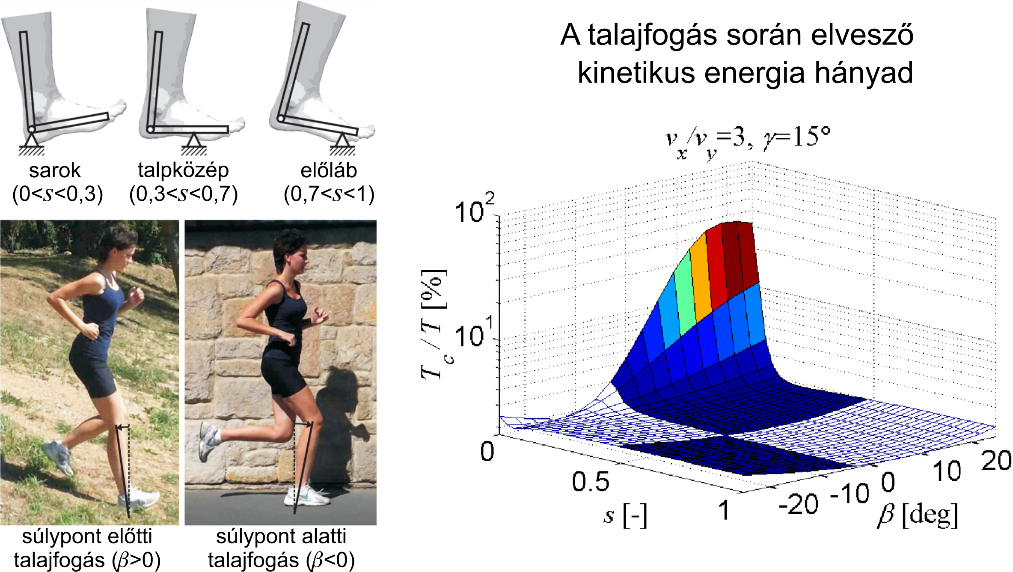
6. ábra. A talaj-láb ütközés elemzése a geometriai paraméterek függvényében
MCs2.4: Digitális hatásokkal kapcsolatos szabályozási hiba becslése
A digitális hatásokkal kapcsolatos szabályozási hiba becslésére rendelkezésre áll egy olyan módszer, mellyel elvileg bármilyen állapot-visszacsatolású lineáris szabályozás hibája becsülhető, ha a szabályozó rendszer kimenete kerekített. A következő pályázati ciklusban az első lépésben a módszer ellenőrzését végezzük el, majd általánosítjuk azt a bemeneti kerekítés – a mért állapot értékek kerekítése – esetére. A végső cél a mind kimeneti, mind bemeneti kerekítés figyelembevétele és a szabályozási hiba becslése a projekt keretében vizsgált összetett, többtest-dinamikai szabályozási feladatok megoldása során.
A várható eredmények jelentősége, alkalmazási lehetőségei
A bonyolult, nagy számítási kapacitást igénylő érintkezési modellek felépítése és az érintkezés modális tulajdonságokra gyakorolt hatásainak elemzése (MCs1.1-MCs1.2) a nemlineáris rezgésdiagnosztikai módszerek pontosságának, megbízhatóságának növelését teszi lehetővé és közvetlen alkalmazást talál a kerék-talaj kapcsolat vizsgálata (MCs1.3) és modellezése (MCs1.4) kapcsán. A felállított komplex gördülési modellek mind a vasúti mind a közúti járművek stabilitásvizsgálatában hasznosíthatók, elősegítve a közlekedésbiztonság növelését.
Az eredmények alapján lehetőség nyílik egész járműszerelvények pontos modellezésére és azok dinamikájának – az alulaktuált rendszerek elméletén alapuló – kifinomult tervezésére (MCs2.1). Az emberi járást és futást imitáló, két lábon járó mobil robotok alulaktuált kialakítása energiahatékony működést tesz lehetővé (MCs2.2). Az ehhez kapcsolódó, talaj-láb ütközés vizsgálatok (MCs2.3) nem csak a robotikában, hanem a sport- és orvostudományban is hasznosítható eredményekre vezetnek, például a sportsérülések elkerülése kapcsán. A digitális hatásokból eredő hiba becslése (MCs2.4) az alulaktuált rendszerek esetében különösen fontos, hogy a „belső”, nem állandóan szabályozott dinamika ne váljon instabillá. Ugyanakkor a „külső” és „belső” dinamika közötti átkapcsolások egy másodlagos digitális hatásként értelmezhetők, így azok stabilitásra gyakorolt hatása is elemezhető a digitális hatásokkal kapcsolatos tapasztalatok alapján.
Várható publikációk
A pályázati ciklus során a kétévente megrendezésre kerülő SIAM - Applications of Dynamical Systems (DS17, DS19, DS21), Dynamical Systems – Theory and Applications (DSTA2017, DSTA2019, DSTA2021) és RoManSy (2018, 2020) konferenciákon, a páros és páratlan években felváltva megrendezett ECCOMAS és ISMD többtest-dinamikai konferenciákon, valamint az ASME-IDETC és Dynamics Days konferenciákon tervezünk részt venni. Emellett évente hat darab folyóirat cikk publikálását tervezzük.
Irodalomjegyzék
- di Bernardo et al: Piecewise Smooth Dynamical Systems, Springer, 2008
- D. Dane Quinn, Daniel Segalman, „Using series-series Iwan-type models for understanding joint dynamics”, ASME J. Appl. Mech., September 2005
- V. L. Popov: Contact Mechanics and Friction – Physical Principles and Applications, Springer, 2010, ISBN 978-3-642-10802-0
- D. Takács, G. Stépán: Micro-shimmy of towed structures in experimentally uncharted unstable parameter domain,, Vehicle System Dynamics, 50:(11) pp. 1613-1630. (2012)
- J.R. Barber, M. Davies, D.A. Hills: Frictional elastic contact with periodic loading, International Journal of Solids and Structures 48, pp. 2041–2047, (2011)
- L. L. Kovács, J. Kövecses, A. Zelei, L. Bencsik and G. Stépán: Servo-Constraint Based Computed Torque Control of Underactuated Mechanical Systems. ASME 2011 8th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Aug. 28-31, 2011, Washington, USA.
- L. L. Kovács, A. Zelei, G. Stépán: Computed torque control of an under-actuated service robot platform modeled by natural coordinates. Communications in Nonlinear Science and Numerical Simulation, 16(5), pp. 2205-2217, (2010).
- G. Csernák: Quantization-induced control error in a digitally controlled system, Nonlinear Dynamics, 85. pp. 2749–2763, (2016)
- Fraunhofer IVI Reverse Driving Assistant: reverse parking with truck-trailer vehicle
- L. Bencsik, A. Zelei: Effects of human running cadence and experimental validation of the bouncing ball model. Mechanical Systems and Signal Processing, August 2016, doi: 10.1016/j.ymssp.2016.08.001.